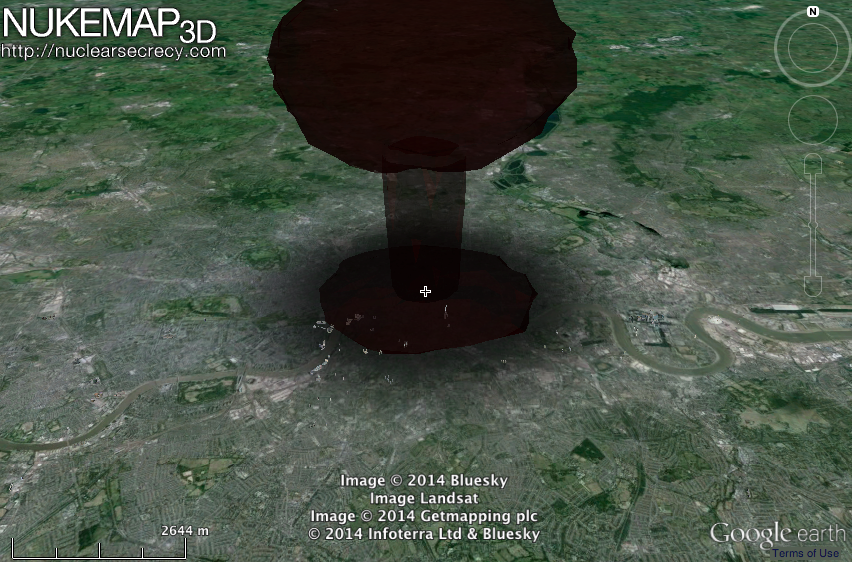
Last night I had a nightmare that the centre of London was nuked. In my half-sleep state I tried working out if I could survive just by getting under my mattress or if I had to get out of bed to be more proactive for my survival.
First, I had to check what kind of bomb could detonate in Piccadilly Circus without destroying my house directly, knowing that I live approximately 6 kilometres away (3.7 miles). According to the wonderful Ground Zero website anything less than 300 Kilotons should leave my house more or less intact.
From the Beer–Lambert–Bouguer law, we know that 1 centimetre of lead absorbs approximately 50% of gamma rays radiation. On the working assumption (that the density is the single characteristic that the absorption coefficient needs) we can estimate that 5 centimetres of brick would act in the same way. To shield me from 50% of the radiation I would need a mattress that is 133 centimetres thick.
Obviously, there plenty of things between me and ground zero so maybe a memory foam mattress 20 cm thick could be enough to save me:
5 percent of the total energy of a nuclear blast is Ionizing radiation. If there was nothing between my house and the explosion we would have about 1020 gamma rays. So, we need to estimate the density of London. My assumption here is that is about twice of the air density, which I think is reasonable. The absorption coefficient for London is 0.16 m-1. Assuming that the distribution of gamma rays is perfectly spherical centred on ground zero, we have
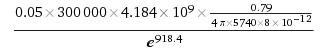
0.05 is the percentage of the Nuclear Energy blast, 300000 is the ton of TNT equivalent, 4.184×109 is the conversion from TNT to Joules, 0.79/(4Pi*5740) is the solid angle that my window spans, 8×10-12 is the energy of a single generic gamma ray photon, e918.4 is the absorption decay.
The exponential term dominates this formula, so no gamma photons will actually reach me. So, I can be happy by simply staying under the duvet and falling asleep again.
Anyway, it’s the radioactive fallout that is going to kill me.